MATEMATICAS: PERMUTACIONES
Definición de permutaciones
Una permutación es el número de maneras distintas en que se pueden ordenar los elementos de un conjunto. Si el conjunto consta de  elementos y estos se quieren disponer en grupos de tamaño
elementos y estos se quieren disponer en grupos de tamaño  , entonces se requiere que
, entonces se requiere que 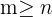 .
.
Hay que tener en cuenta lo siguiente:
1 Sí importa el orden de los grupos, ya que el intercambio entre dos elementos distintos genera una nueva permutación
2 No se repiten los elementos, ya que de repetirse o ser iguales entre si, al intercambiarlos no se genera una nueva permutación
Para obtener el total de maneras en que se pueden colocar  elementos en
elementos en  posiciones se utiliza la siguiente fórmula:
posiciones se utiliza la siguiente fórmula:

Si en dado caso, 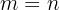 para calcular el total de permutaciones se utiliza la siguiente fórmula:
para calcular el total de permutaciones se utiliza la siguiente fórmula:
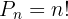
A continuación, analiza los siguientes ejemplos utilizando lo anteriormente mencionado.
Ejemplos de problemas de permutaciones
1Calcular las permutaciones de  elementos en
elementos en  posiciones.
posiciones.
Solución:
En este caso 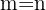 por lo que empleamos
por lo que empleamos
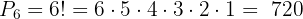
Así, hay  formas distintas de acomodar
formas distintas de acomodar  elementos.
elementos.
2¿Cuántos números de 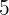 cifras diferentes se pueden formar con los dígitos:
cifras diferentes se pueden formar con los dígitos: 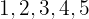 ?
?
Solución:
Como se tiene  dígitos diferentes, y se quiere números de cinco cifras, entonces
dígitos diferentes, y se quiere números de cinco cifras, entonces 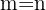 por lo que empleamos
por lo que empleamos

Así, hay  números de cinco cifras distintos formados con los dígitos
números de cinco cifras distintos formados con los dígitos  .
.
3¿De cuántas formas distintas pueden sentarse ocho personas en una fila de ocho butacas?
Solución:
Como se tiene  personas y estas son diferentes, ya que no nos indican que hayan dos iguales y se quieren sentar en ocho butacas, entonces
personas y estas son diferentes, ya que no nos indican que hayan dos iguales y se quieren sentar en ocho butacas, entonces 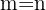 por lo que empleamos
por lo que empleamos
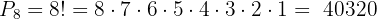
Así, hay 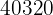 formas distintas de sentar a ocho personas en ocho butácas.
formas distintas de sentar a ocho personas en ocho butácas.
4¿De cuántas formas distintas pueden sentarse ocho personas en una fila de siete butacas?
Solución:
Como se tiene  personas y estas son diferentes, ya que no nos indican que hayan dos iguales y se quieren sentar en
personas y estas son diferentes, ya que no nos indican que hayan dos iguales y se quieren sentar en  butacas, entonces
butacas, entonces  por lo que empleamos
por lo que empleamos
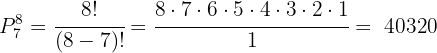
Así, hay 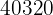 formas distintas de sentar a ocho personas en siete butácas. Esto se debe a que siempre queda una persona sin sentar.
formas distintas de sentar a ocho personas en siete butácas. Esto se debe a que siempre queda una persona sin sentar.
5¿De cuántas formas distintas pueden sentarse ocho personas en una fila de cinco butacas?
Solución:
Como se tiene  personas y estas son diferentes, ya que no nos indican que hayan dos iguales y se quieren sentar en
personas y estas son diferentes, ya que no nos indican que hayan dos iguales y se quieren sentar en  butacas, entonces
butacas, entonces  por lo que empleamos
por lo que empleamos
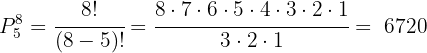
Así, hay 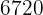 formas distintas de sentar a ocho personas en cinco butácas.
formas distintas de sentar a ocho personas en cinco butácas.
6¿Cuántas formas diferentes hay de colocar a las letras  en tres posiciones?
en tres posiciones?
Solución:
En este caso 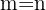 por lo que empleamos
por lo que empleamos

Así, hay  formas distintas de acomodar las letras
formas distintas de acomodar las letras 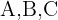 elementos y estas son:
elementos y estas son:

7Si tenemos a  elementos y queremos colocarlos en
elementos y queremos colocarlos en 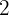 posiciones, ¿de cuántas maneras se puede realizar?
posiciones, ¿de cuántas maneras se puede realizar?
Solución:
En este caso  por lo que empleamos
por lo que empleamos
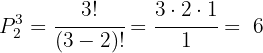
Así, hay  formas distintas de acomodar tres elementos en dos posiciones. Si denotamos a los elementos con las letras
formas distintas de acomodar tres elementos en dos posiciones. Si denotamos a los elementos con las letras 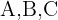 las distintas formas de acomodarlas en dos posiciones son:
las distintas formas de acomodarlas en dos posiciones son:
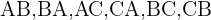
8Si tenemos 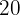 alumnos y queremos formar una comisión de
alumnos y queremos formar una comisión de  alumnos, ¿cuántas comisiones distintas podemos realizar?
alumnos, ¿cuántas comisiones distintas podemos realizar?
Solución:
En este caso  por lo que empleamos
por lo que empleamos
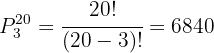
Así, hay 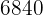 formas distintas de acomodar veinte alumnos en comisiones de tamaño tres.
formas distintas de acomodar veinte alumnos en comisiones de tamaño tres.
Comentarios
Publicar un comentario