MATEMATICAS: MAGNITUDES DIRECTAMENTE PROPORCIONALES
Definición de proporcionalidad directa
Dos magnitudes son directamente proporcionales cuando, al multiplicar una de ellas por un número cualquiera, la otra queda multiplicada por el mismo número. Igualmente, dos magnitudes son directamente proporcionales si, al dividir una por cualquier número, entonces la otra queda dividida por el mismo número.
Se establece una relación de proporcionalidad directa entre dos magnitudes cuando:
- A más cantidad de la primera magnitud, corresponde más cantidad en la segunda magnitud, en la misma proporción.
- A menos cantidad en la primera magnitud, corresponde menos cantidad en la segunda magnitud, en la misma proporción.
Otra manera de determinar si dos magnitudes son directamente proporcionales es por medio de su cociente. El cociente entre dos magnitudes directamente proporcionales siempre es constante.
Ejemplos de problemas de proporcionalidad directa
Ahora, veamos algunos ejemplos de cantidades directamente proporcionales:
1 El peso de un producto y su precio son dos magnitudes directamente proporcionales.
Observemos que si 
kg de tomates cuesta 
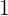, entonces:
kg de tomates costará 
kg de tomates costará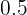 
(
céntimos)
Es decir, por más kilogramos de tomate se pagarán más euros. Asimismo, por menos kilogramos de tomate se pagará menos euros. Notemos, además, que dividir el peso entre el precio siempre nos da como cociente.
2 Otros ejemplos de magnitudes directamente proporcionales son:
- La distancia recorrida por un automóvil y el tiempo empleado en recorrer esa distancia —recorrer el doble de distancia implica emplear el doble de tiempo—.
- El volumen de un cuerpo y su peso —un cuerpo con doble de volumen pesará el doble, siempre que esté hecho del mismo material—.
- La cantidad de caramelos y el precio a pagar por ellos —pagarás el doble de euros para comprar el doble de caramelos—.
1. Un panadero puede hacer 50 panes en 2 horas. ¿Cuántos panes podrá hacer en 6 horas si sigue al mismo ritmo?
a) 100
b) 150
c) 200
d) 250
2. Si 3 panaderos hacen 120 panes en 4 horas, ¿cuántos panes podrán hacer 5 panaderos en el mismo tiempo?
a) 180
b) 200
c) 300
d) 400
3. Un panadero utiliza 2 kg de harina para hacer 40 panes. ¿Cuántos kg de harina necesitará para hacer 100 panes?
a) 3 kg
b) 4 kg
c) 5 kg
d) 6 kg
4. Si con 1 kg de azúcar se hacen 80 panes, ¿cuántos panes se pueden hacer con 3 kg de azúcar?
a) 160 panes
b) 200 panes
c) 240 panes
d) 300 panes
5. Un panadero hornea 60 panes en 3 horas. Si trabaja durante 9 horas al mismo ritmo, ¿cuántos panes horneará?
a) 120
b) 180
c) 240
d) 300
Tema 2: Pintor pintando casas
6. Un pintor puede pintar 2 casas en 5 días. Si pinta 6 casas, ¿cuántos días necesitará?
a) 10 días
b) 12 días
c) 15 días
d) 18 días
7. Si un pintor tarda 4 días en pintar 3 casas, ¿cuántos días tardará en pintar 9 casas al mismo ritmo?
a) 8 días
b) 10 días
c) 12 días
d) 15 días
8. Un pintor usa 10 litros de pintura para pintar 2 casas. ¿Cuántos litros de pintura necesitará para pintar 5 casas?
a) 15 litros
b) 20 litros
c) 25 litros
d) 30 litros
Tema 3: Hombre comiendo hamburguesas
9. Un hombre se come 3 hamburguesas en 15 minutos. Si sigue comiendo al mismo ritmo, ¿cuántas hamburguesas comerá en 45 minutos?
a) 6
b) 9
c) 12
d) 15
10. Si 4 hombres comen 20 hamburguesas en 30 minutos, ¿cuántas hamburguesas comerán 6 hombres en el mismo tiempo?
a) 25
b) 30
c) 35
d) 40
Comentarios
Publicar un comentario